前言
在上节课中我们见过了一些不可判定语言的例子:$DIAG$是非半可判定的,并且因此也是不可判定的,而$A_{DTM}$和$HALT$是半可判定的,但却是不可判定的。这节课我们将会看多看一些例子。我们也将引入语言约化(reduction)的概念,它可以用来证明语言的不可判定性。
然而在此之前,我们将会花一些时间来观察几个设计图灵的好用的基本技巧。
知识点
几个基本的图灵机技巧
这个小节包含了两个用来证明语言不可判定性(或者非半可判定性)的思路,也适用于其他情况。第一个涉及到一种简单的方法来管理无限域的搜索,而第二个则是关于强大的图灵机硬编码输入技术。
限制无限搜索空间
有时候我们想要图灵机能在无限的空间中高效搜索,但是这不是显而易见就能做到的。解决这个问题的一种方法是建立一个循环,在这个循环中,单个正整数同时作为搜索空间中多个参数的边界。
下面这个定理的证明,本身它也很重要,阐明了这个思路。
定理17.1. 已知$\Sigma$是一个字母表,$A\subseteq \Sigma^{*}$是一个语言,而且$A$和$\overline{A}$都是半可判定的。语言$A$是可判定的。
证明:因为$A$和$\overline{A}$都是半可判定语言,一定存在DTM $M_0$和$M_1$使得$A=L(M_0)$和$\overline{A}=L(M_1)$。定义一个新的DTM $M$如图17.1所示。
现在让我们DTM $M$输入一个已知字符串$w$的行为。如果$w\in A$,那么$M_0$最终会接受$w$,而$M_1$则不会。($M_1$可能会拒绝,也可能一直运行,但它不可能接受$w$)。因此导致了$M$接受$w$。相反,如果$w\notin A$,那么$M_1$最终会接受$w$,而$M_0$则不会,并且因此$M$拒绝$w$。结果,$M$判定了$A$,所以$A$是可判定的,证毕。
明确一点,图17.1描述DTM $M$所使用的变量$t$就是前面提到的限制技术;它是一个单一变量,但同时用来限制了$M_0$和$M_1$(在步骤2和3中)的模拟,所以两者都不会一直执行。关于这个技术我们在下节课的例子中会看到进一步的使用。
硬编码输入字符串
假设我们有一个DTM $M$以及其字母表符号组成的字符串$x$。考虑一个新的DTM $M_x$如图17.2所示。
看起来这个图灵机是没啥用处的:$M_x$总是忽略输入字符串得到同样的输出。本质上,输入字符串$x$就是被“硬编码”了到了$M_x$的描述中。然而,我们会发现有时候这样定义一个DTM还是有用处的,特别是我们在证明某个语言的不可判定性或者非半可判定性时。
我们也注意到如果我们有DTM $M$以及输入字母表字符串组成的字符串$x$的编码$\langle\langle M\rangle,\langle x\rangle\rangle$,不难计算出DTM $M_x$的编码$\langle M_x\rangle$。DTM $M_x$可以描述为下面三个阶段:
- 将磁头移动到输入字符串的右侧,将$w$的符号用空格替换,直到$w$被擦除。
- 从字符串$x$的末尾开始,依次输入$x$的符号,并且磁头往左移动。
- 一旦字符串$x$被写入磁带,将控制权交还给$M$。
第一个阶段使用两个状态很容易完成,第二个阶段分别将$x$的每个字符对应$M_x$的一个状态也能完成。第三个阶段的操作就和$M$一模一样了。图17.3描述了DTM $M_{0011}$的状态图。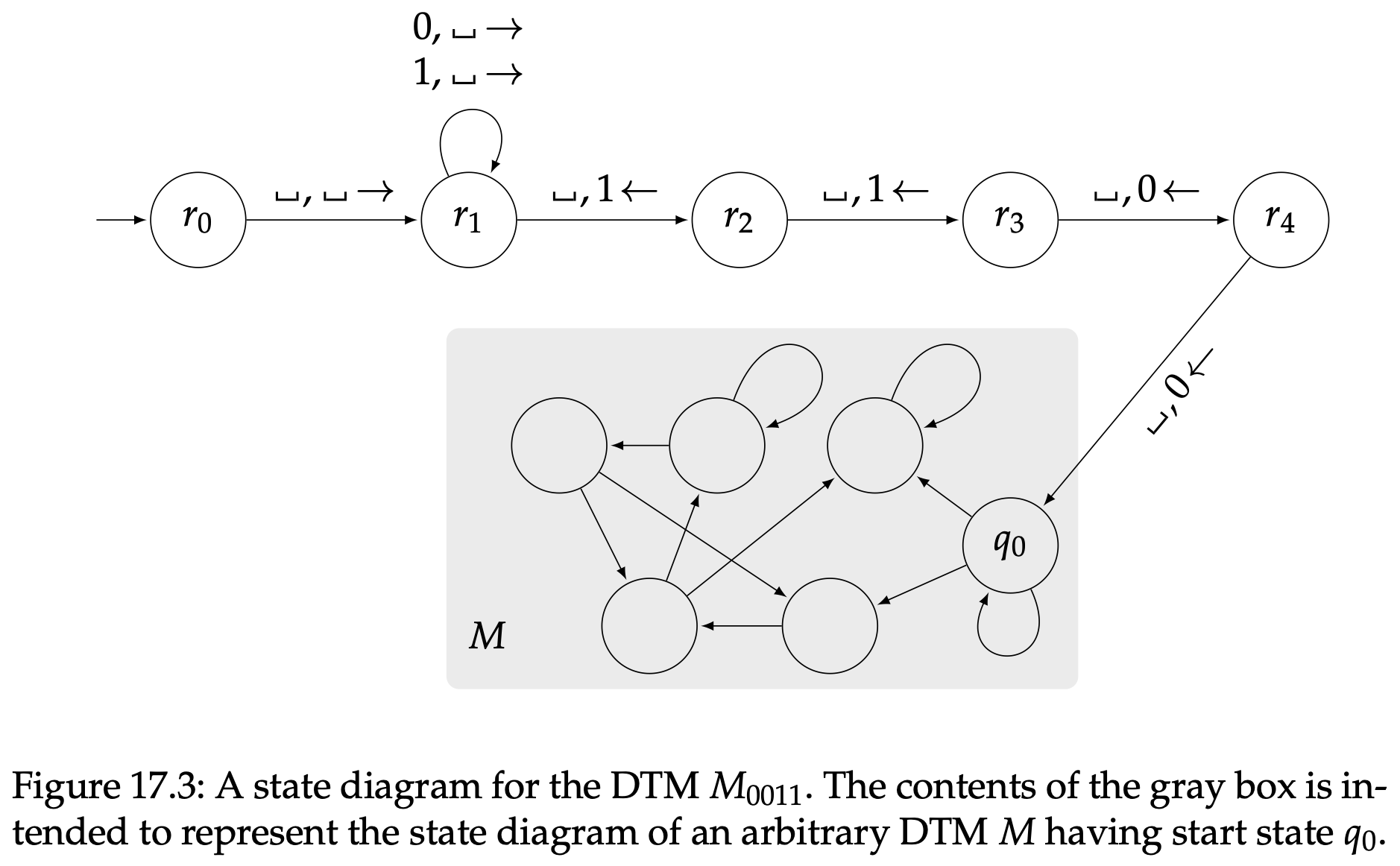
这里有个例子正好可以用来讲讲这个无用的构造。定义一个语言
命题17.2. 语言$E_{DTM}$是不可判定的。
证明:使用反证法,假设$E_{DTM}$是可判定的,所以存在一个DTM $T$可以判定这个语言。定义一个新的DTM $K$如图17.4所示。
现在,假定$M$是一个DTM并且$x\in L(M)$,来看$K$输入$\langle\langle M\rangle,\langle x\rangle\rangle$后的行为。因为$M$接受$x$,$M_x$接受任意基于它的字母表的字符串 — 因为不管你输入什么都会被擦掉,然后执行输入$x$,导致结果被接受。因此得出$L(M_x)\neq\varnothing$,所以$T$一定拒绝$M_x$,并且因此$K$接受$\langle\langle M\rangle,\langle x\rangle\rangle$。
相反,如果$M$是一个DTM并且$x\notin L(M)$,那么$K$将会拒绝输入$\langle\langle M\rangle,\langle x\rangle\rangle$。不是因为$x$包含了$M$的字母表以外的字符,就是因为$M$拒绝或者永远运行。在第二种情况下,$M_x$决绝或者永远运行每个字符串,因此$L(M_x)=\varnothing$。因此DTM $T$接受$\langle M_x\rangle$,导致$K$拒绝输入$\langle\langle M\rangle,\langle x\rangle\rangle$。
这样,$K$就判定了$A_{DTM}$,但我们已知这个语言是不可判定的。因此出现了矛盾,我们得到$E_{DTM}$是不可判定的,证毕。
使用约化证明不可判定性
目前我们证明一个语言的不可判定性或者非半可判定性都遵循了一个模式,为了证明某个语言$A$是不可判定的:
- 使用反证法,假设$A$是可判定的。
- 利用这个假设构造一个$DTM$来判定语言$B$,但我们已知$B$是不可判定的。
- 得到最初假设的矛盾,我们得出$A$是不可判定的。
同样的方法有时候也能用来证明$A$是非半可判定的,通过假设$A$是可判定的,加上一个已知非半可判定语言$B$,得到矛盾。
约化
事实上约化这个概念非常普遍,在理论计算机科学中有多种类型 — 但是我们要讲的只是其中一种(有事我们称之为映射约化
定义17.3. 已知$\Sigma$和$\Gamma$是字母表,$A\subseteq\Sigma^{*}$和$B\subseteq^{*}$是语言。据说$A$约化为$B$的条件是存在一个可以算函数$f:\Sigma^{*}\rightarrow \Gamma^{*}$使得
其中所有$w\in\Sigma^{*}$。我们常用$A\leq_m B$来表示$A$约化为$B$,并且任意能完成这个任务的函数我们都称之为一个$A$到$B$的约化。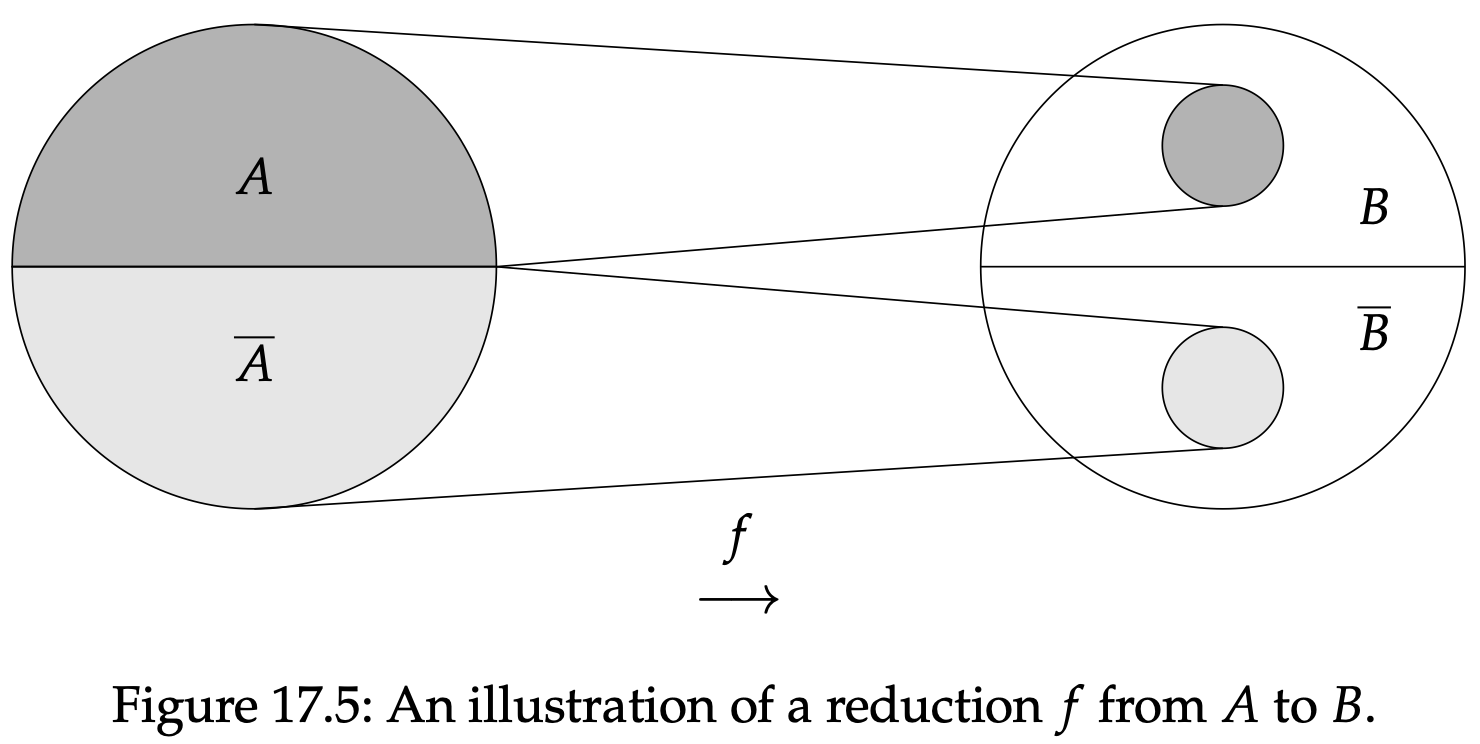
图17.5阐述了一个约化的活动。直观来说,约化是一种将一个可计算判定问题转变成另一个的方式。想象一下,你收到了一个输入字符串$w\in\Sigma^{*}$,你想要判断是否$w$包含于某个语言$A$。也许你不知道如何去判断,但是恰好你有个朋友能够判断某个字符串$y\in\Gamma^{*}$是否包含于一个不同的语言$B$。如果你有一个从$A$到$B$的约化$f$,那么你就可以通过朋友的帮助来判是否$w\in A$:你计算出$y=f(w)$,问你的朋友是否$y\in B$,他的答案就能直接告诉你是否$w\in A$。
接下来这个定义有一个简单直接的证明,但是它却非常的重要,因为它是我们推断可判定性和半可判定性的关键。
定理17.4. 已知$\Sigma$和$\Gamma$是字母表,$A\subseteq\Sigma^{*}$和$B\subseteq\Gamma^{*}$是语言,并且假设$A\leq_m B$。有以下两个含义:
- 如果$B$是可判定的,那么$A$也是可判定的。
- 如果$B$是半可判定的,那么$B$也是半可判定的。
证明:让$f:\Sigma^{*}\rightarrow\Gamma^{*}$作为一个$A$到$B$的约化。我们知道这个函数的存在是因为$A\leq_m B$。
我们先证明第二个含义。因为$B$是半可判定的,一定存在一个DTM $M_B$使得$B=L(M_B)$。定义一个新的DTM $M_A$如图17.6。像这样定义一个DTM是可行的,因为$f$是一个可计算函数。
对于一个输入字符串$w\in A$,我们有$y=f(w)\in B$,这点由约化$f$给我们提供保证。当$M_A$执行输入$w$,它会接受,因为$M_B$会接受$y$。同样,如果$w\notin A$,那么$y=f(w)\notin B$。当$M_A$执行输入$w$,它不会接受,因为$M_B$不会接受$y$(也许会拒绝或者永远执行,但是我们并不关心)。这样我们确立了$A=L(M_A)$,并且因此$A$是半可判定的。
第一个含义的证明也几乎相同,除了我们需要让$M_B$是一个可以判定$B$的DTM。这个DTM $M_A$的定义也在图17.6中,并且可以判定A,那么$A$是可判定的。
很快我们将会用到这个定理来证明某个语言是不可判定的(或者非半可判定的),但是在此之前我们先来观察两个关于约化的实用推理。
命题17.5. 已知$\Sigma、\Gamma和\Delta$是字母表,$A\subseteq \Sigma^{*}、B\subseteq\Gamma^{*}和C\subseteq\Delta^{*}$是语言。如果$A\leq_m B$并且$B\leq_m C$,那么$A\leq_m C$。(用文字表达,$\leq_m$在语言之间是一种传递关系)
证明:因为$A\leq_m B$和$B\leq_m C$,一定存在可计算函数$f:\Sigma^{*}\rightarrow\Gamma^{*}$和$g:\Gamma^{*}\rightarrow\Delta^{*}$使得
其中所有$w\in\Sigma^{*}$和$y\in\Gamma^{*}$。
定义一个函数$h:\Sigma^{*}\rightarrow\Delta^{*}$,对于所有$w\in\Sigma^{*}$都有$h(w)=g(f(w))$。很明显$h$是一个可计算函数:如果我们有DTM $M_f$和$M_g$分别计算$f$和$g$,那么我们就能通过先执行$M_f$再执行$M_g$获得DTM $M_h$。
剩下就是来看$h$怎么把$A$约化成$C$。如果$w\in A$,那么$f(w)\in B$,那么因此$h(w)=g(f(w))\in C$;如果$w\notin A$,那么$f(w)\notin B$,那么因此$h(w)=g(f(w)\notin C$。
命题17.6. 已知$\Sigma$和$\Gamma$是字母表,$A\subseteq\Sigma^{*}$和$B\subseteq\Gamma^{*}$是语言。那么$A\leq_m B$当且仅当$\overline{A}\leq_m\overline{B}$。
证明:对于一个已知函数$f:\Sigma^{*}\rightarrow\Gamma^{*}$和一个字符串$w\in\Sigma^{*}$,声明$w\in A\Leftrightarrow f(w)\in B$和$w\in\overline{A}\Leftrightarrow f(w)\in\overline{B}$是逻辑等价的。如果我们有一个从$A$到$B$的约化$f$,那么同样的函数也能做到从$\overline{A}$到$\overline{B}$的约化,并且反之亦然。
不可判定性的约化
我们能够使用定理17.4来证明某个语言是可判定的或者半可判定的,但是我们主要是用它来证明语言的不可判定性和非半可判定性。当我们这样使用这个定理时,我们要把它的两个含义改成对应的形式。也就是,如果两个语言$A\subseteq\Sigma^{*}$和$B\subseteq^{*}$满足$A\leq_m B$,那么它有以下两个含义:
- 如果$A$是不可判定的,那么$B$也是不可判定的。
- 如果$A$是非半可判定的,那么$B$也是非半可判定的。
所以,如果我们想要证明某个语言$B$是不可判定的,那么你只要找到任意已知是不可判定的语言$A$,然后证明$A\leq_m B$就足够了。证明语言的非半可判定性也是类似的。接下来的例子会告诉你具体怎么做。
案例17.7. 第一个约化的例子,我们将证明

首先我们要考虑的事情是找到一种方法改造DTM $M$得到一个不同的DTM。具体一点,对于任意DTM $M$,让我们定义一个DTM $K_M$如图17.7。DTM $K_M$的思路很简单:如果$M$接受一个字符串$w$,那么$K_M$也接受,如果$M$拒绝$w$,那么$K_M$就一直运行。这样,$K_M$输入$w$后停止当且仅当$M$接受$w$。注意如果你有关于DTM $M$的描述,很容易就能设计一个DTM $K_M$的描述,做法就是:把$M$的拒绝状态替换成一个新的状态,造成一个无限循环(比如不停地右移磁头)。
现在让我们定义一个函数$f:\{0,1\}^{*}\rightarrow\{0,1\}^{*}$如下:
其中$x_0\in\{0,1\}^{*}$是任意不包含于$HALT$的已知字符串。(比如,我们可以让$x_0=\varepsilon$,因为$\varepsilon$中并没有包含一个DTM的编码 — 但是我们并不关心这一点,只要它不属于$HALT$就行)函数$f$是可计算的:它先检查输入字符串编码$\langle\langle M\rangle,\langle w\rangle\rangle$的格式,$M$必须是一个DTM,且$w$由$M$的字母表字符组成,如果是这样就把$M$的编码替换成上述的DTM $K_M$的编码。
现在让我们来检验$f$能否从$A_{DTM}$约化成$HALT$。首先假设我们有一个输入$\langle\langle M\rangle,\langle w\rangle\rangle\in A_{DTM}$。它有以下含义:
因此我们得到
关于$f$确实是一个从$A_{DTM}$到$HALT$的约化,我们已经验证了一半。
剩下的就是考虑不包含于$A_{DTM}$的输入通过$f$得到的输出,这里有两种情况:一种情况是$\langle\langle M\rangle,\langle w\rangle\rangle$的格式满足$M$是一个DTM且$w$是由$M$的字母表字符组成,另外一种情况则不是。对第一种情况,它有以下含义:
这里的关键是$K_M$的定义明确说了如果$M$不接受就会一直运行(无视$M$到底是拒绝还是一直运行)。最后这个情况是我们有一个字符串$x\in\Sigma^{*}$格式不满足$M$是一个DTM且$w$是由$M$的字母表字符组成,这种情况我们直接得到$f(x)=x_0\notin HALT$。(这也是为什么我们会为$f$的定义加入这种情况,往后类似的例子我们也会这么做)
因此我们证明了
并且得到$A_{DTM}\leq_m HALT$。
虽然我们已经证明过$HALT$是不可判定的,但是$A_{DTM}\leq_m HALT$为我们提供了另一种证明:因为我们已知$A_{DTM}$是不可判定的,也就是说$HALT$也是不可判定的。
也许对比我们上节课$HALT$不可判定的证明,这个证明没看出有啥优势。但是相较于之前我们建立一种$A_{DTM}$和$HALT$的亲密关系。一般来说,有时候使用约化来证明语言的不可判定性(或者非半可判定性)是一种捷径。
案例17.8. 下一个约化的例子,我们将会证明
其中我们回看一下$E_{DTM}$的定义是:
现在我们来证明$DIAG\leq_m E_{DTM}$。因为我们已经知道$DIAG$是非半可判定的,有这个约化可知$E_{DTM}$不仅是不可判定的,也是非半可判定的。
这个例子我们将会再次用到本节课开篇提到的硬编码手段:对于一个已知的DTM $M$,让我们定义一个新的DTM $M_{\langle M\rangle}$如图17.2,指定硬编码字符串$x=\langle M\rangle$。这需要$M$的输入字母表包含编码$\langle M\rangle$使用的符号$\{0,1\}$才有意义,所以我们认同如果不是这样,$M_{\langle M\rangle}$就直接拒绝。
现在让我们定义一个函数$f:\{0,1\}^{*}\rightarrow \{0,1\}^{*}$如下:
其中$x_0$是不包含于$E_{DTM}$的任意二进制字符串。如果你思考一会儿,不难说服自己$f$是可计算的。剩下的就是验证$f$是一个从$DIAG$到$E_{DTM}$的约化。
对于任意字符串$x\in DIAG$,我们已知对于某个DTM $M$有$x=\langle M\rangle$满足$\langle M\rangle\notin L(M)$。这种情况我们计算出$f(x)=\langle M_{\langle M\rangle}\rangle$,因为$\langle M\rangle\notin L(M)$,因此$M_{\langle M\rangle}$永远都不会接受,所以$f(x)=\langle M_{\langle M\rangle}\rangle\in E_{DTM}$。
现在假设$x\notin DIAG$。这里有两种情况:要么$x$是一个DTM的编码并且$\langle M\rangle\in L(M)$,要么就是$x$根本不是一个DTM的编码。如果是第一种情况,$M_{\langle M\rangle}$接受每个基于它字母表的输入字符串,因此$f(x)=\langle M_{\langle M\rangle}\rangle\notin E_{DTM}$。如果是第二种情况,那么我们直接得到$f(x)=x_0\notin E_{DTM}$。
我们证明了
如此$DIAG\leq_m E_{DTM}$的证明就完成了。
案例17.9. 我们第三个约化的例子是
其中语言$AE$的定义是
取名$AE$代表的意思是”accept the empty string.”
证明这个约化,我们同样可以使用硬编码手法,现在我们已经用过两次了。对于每个DTM $M$和基于$M$字母表的字符串$x$,定义一个新的DTM $DTM M_x$如图17.2,定义一个函数$f:\{0,1\}^{*}$\rightarrow \{0,1\}^{*}如下:
正如你所想的,其中$w_0$是任意不包含于$AE$的已知字符串。现在让我们验证$f$是一个从$A_{DTM}$到$AE$的有效约化。
首先,对于任意字符串$w\in A_{DTM}$,我们有$w=\langle\langle M\rangle,\langle x\rangle\rangle$,其中$M$是一个接受字符串$x$的DTM。这种情况,$f(w)=\langle M_x\rangle$。我们知道$M_x$接受每一个输入字符串,包括空字符串,因为$M$接受$x$,因此$f(w)=\langle M_x\rangle\in AE$。
现在考虑任意字符串$w\notin A_{DTM}$,有两种情况。如果$w=\langle\langle M\rangle,\langle x\rangle\rangle$中$M$是一个DTM并且$x$的字符也来自$M$的字母表,那么$w\notin A_{DTM}$,也就是说$M$不接受$x$。这种情况我们得到$f(w)=\langle M_x\rangle\notin AE$,因为$M_x$不接受任何字符串(包括空字符串)。如果第二种情况$x$的格式不对,那么$f(w)=w_0\notin AE$。
我们证明了对于任意字符串$w\in\{0,1\}^{*}$都存在$w\in A_{DTM}\Leftrightarrow f(w)\in AE$,因此也就得到了$A_{DTM}\leq_m AE$,证毕。
案例17.10. 最后这个关约化的例子相较于其他几个就比较难了。我们将要证明
其中
注意$\langle M\rangle \in DEC$并不表示$M$总会停止 — 但可以说存在一个DMT $K$,不一定是$M$。
已知任意一个DTM $M$,让我们定义一个新的DTM $K_M$如图17.8所示。在这个描述中,假设$H$是一个任意已知的DTM并且满足$L(H)=HALT$。我们知道这样的$H$是存在的;我们可以简单采用一个通用DTM $\mathfrak{U}$,他可以半可判定HALT。如果有人想问为什么我们这样定义$K_M$,只能说答案就是这样做能让约化起作用 — 注意在$K_M$的定义中我们用到了这节课开篇提到的无限搜索技巧。
现在让我们定义一个函数$f:\{0,1\}^{*}\rightarrow \{0,1\}^{*}$如下
其中$x_0$是一个已知不包含于$DEC$的二进制字符串。这是一个可计算的函数,接下来我们要验证它是一个从$E_{DTM}$到$DEC$的约化。
假设$\langle M\rangle\in E_{DTM}$。因此我们得到了$L(M)=\varnothing$;再来看$K_M$的行为我们也得到$L(K_M)=\varnothing$;如果$M$不接受,计算会在第2步和第3步之间一直交替执行。空语言是可以判定的,因此$f(\langle M\rangle)=\langle K_M\rangle\in DEC$。
相反,如果$M$是一个DTM并且$\langle M\rangle\notin E_{DTM}$,那么$M$至少会接受一个字符串。这表示$L(K_M)=HALT$,因为$K_M$最终会找到一个能被$M$接受的字符串,到达第4步,然后接受当且仅当$x\in HALT$。因此$f(\langle M\rangle)=\langle K_M\rangle\notin DEC$。剩下的情况就是$x$不是一个DTM编码,这种情况直接得出$f(x)=x_0\notin DEC$。
我们证明了对于任意字符串$x\in\{0,1\}^{*}$都存在$x\in E_{DTM}\Leftrightarrow f(x)\in DEC$,因此得到了$E_{DTM}\leq_m DEC$,证毕。
因为我们一直$E_{DTM}$是非半可判定的,我们得出结论:语言$DEC$也是非半可判定的。